Для сучасного школяра не становить праці побудувати правильний багатокутник. Кожен може накреслити трикутник, квадрат, п'ятикутник... Навіть якщо число сторін зросте до декількох десятків, рішення задачі потребує лише трохи більше терпіння і посидючості. Але що робити, якщо мова зайде про тисячі і десятки тисяч сторін?
В університеті німецького міста Геттінгена стався випадок з розряду курйозних. Про нього розповів відомий англійський математик Д. Литтлвуд. Один не в міру нав'язливий аспірант вивів свого керівника з терпіння. Бажаючи хоч трохи відпочити від допитливого учня, професор сказав йому: «Ідіть і розробіть побудова правильного багатокутника з 65 357 сторонами».
Професор надовго позбавився від учня, адже старанний німець взяв завдання керівника всерйоз. Він повернувся тільки через 20 років з відповідною побудовою. І зараз це диво посидючості зберігається в архівах Геттінгенського університету.
Інші джерела говорять, що ця історія - всього лише жарт, придумана Литтлвудом на основі реальної події: побудова дійсно існує і його оригінал насправді зберігається в бібліотеці Геттінгенського університету. Це побудова справив математик Йоганн Густав Гермес в 1894 році, витративши на це понад 10 років. Рукопис займає більше 200 сторінок, міститься у величезному валізі і через своїх неосяжних розмірів ніколи не була опублікована.
До речі...
Чому саме 65 537 сторін? Зрозуміло, професор взяв не зі стелі. Справа в тому, що ще в 1836 році видатний німецький математик Карл Фрідріх Гаусс довів, що правильний многокутник можна побудувати, користуючись лише циркулем і лінійкою, якщо кількість його вершин одно простого числа Ферма, тобто числа виду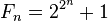 
, де n - невід'ємне ціле число.
А 65 537 - це найбільше з відомих чисел Ферма:
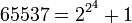
Як же виглядає це чудо людської думки - шестидесятипятитысячпятисоттридцатисемиугольник? Зовні він практично не відрізняється від кола! Адже його центральний кут, тобто кут з вершиною в центрі кола, мізерно малий - 0°0'19"77508888. Якщо намалювати 65537-кутник з довжиною однієї сторони 1 см, то його діаметр буде більше 200 м.
