Серед читачів цієї книги, без сумніву, знайдуться і такі, які забажають самі перевірити розрахунки, згадані вище. Наводимо тут ці обчислення. Вони вірні лише приблизно, оскільки засновані на припущенні, що в каналі гармати снаряд рухається рівномірно-прискорено (насправді ж зростання швидкості відбувається нерівномірно).
Для розрахунків доведеться користуватися наступними двома формулами рівномірно-прискореного руху:
швидкість v після закінчення t-ї секунди дорівнює at, де а - прискорення:
v = at;
шлях S, пройдений за t секунд, визначається формулою
S = at2/2.
За цими формулами визначимо перш за все прискорення снаряду, коли він ковзав в каналі «колумбиады».
З роману відома довжина частини гармати, не зайнятої зарядом, - 210 м; це і є пройдений снарядом шлях S.
Ми знаємо і кінцеву швидкість: v =16 000 м/с. Дані S і v дозволяють визначити величину t - тривалість руху снаряда в каналі знаряддя (розглядаючи це рух як рівномірно-прискорений). У насправді:
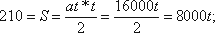
v = at = 16000,
звідки
t = 210/8000 = близько 1/40 сек.
Снаряд, виявляється, ковзав б всередині гармати всього 1/40 секунди! Підставивши
t = 1/40 у формулу v = at, маємо:
16 000 = 1/40 а, звідки а = 640 000 м/с2.
Отже, прискорення снаряду при русі в каналі дорівнює 640 000 м/с2, тобто в 64 000 разів більше прискорення сили тяжкості!
Якої ж довжини повинна бути гармата, щоб прискорення снаряду було всього у 10 разів більше прискорення падаючого тіла (тобто дорівнювало б 100 м/с2)?
Це - задача, обернена тій, яку ми зараз вирішили. Дані:
a = 100 м/с2,
v =11 000 м/с (при відсутності опору атмосфери така швидкість достатня).
З формули v = at маємо:
11000 = 100t, звідки t = 110 с.
З формули S = at2/2 отримуємо, що довжина гармати повинна дорівнювати
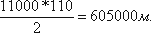
тобто круглим рахунком 600 км.
Такими обчисленнями отримані ті цифри, які руйнують привабливі плани героїв Жюля Верна.