Але невже ламаний шлях може найшвидше привести до мети, ніж прямий? Так, в тих випадках, коли швидкість руху в різних частинах шляху різна. Згадайте, що доводиться робити жителям села, що розташована між двома залізничними станціями в сусідстві з однією з них. Щоб швидше потрапити на далеку станцію, вони їдуть на коні спочатку в зворотному напрямку, до найближчої станції, там сідають в поїзд і їдуть на місце призначення. Їм коротше було б, зрозуміло, прямо їхати туди на коні, але вони віддають перевагу більш довгий шлях на коні й у вагоні, тому що він приводить до мети скоріше.
Приділимо хвилину уваги ще одному прикладу. Кавалерист повинен прибути з донесенням з точки А до намету командира в точці C (див. рис.). Його відокремлюють від намету смуга глибокого піску і смуга луки, розмежовані між собою прямою лінією EF, По піщаному ґрунті кінь рухається вдвічі повільніше, ніж по лузі. Який же шлях повинен вибрати кавалерист, щоб досягти намети в найкоротший час?

Задача про кавалеристе. Знайти швидкий шлях з A в С.
На перший погляд здається, що самий швидкий шлях - пряма лінія, проведена від A до С. Але це зовсім помилково, і я не думаю, щоб знайшовся кавалерист, який обрав такий шлях. Повільне рух по піску наведе його на правильну думку скоротити цю повільну частину шляху, прорізавши піщану смугу менш косій лінії; звичайно, тим самим подовжиться друга частина шляху - по лузі; але так як по лузі можна рухатися удвічі швидше, то подовження шляху не переважить отриманої вигоди, і в загальному підсумку шлях буде пройдений в менший проміжок часу. Іншими словами, шлях кавалериста повинен переломитися на кордоні обох пологів грунту і притому так, щоб шлях по лузі становив з перпендикуляром до межі більший кут, ніж шлях по піщаному ґрунті.
Хто знайомий з геометрією, саме з теоремою Піфагора, той може перевірити, що прямий шлях AC дійсно не є якнайшвидшим шляхом і що при тих розмірах ширини смуг і відстаней, які ми тут маємо на увазі, можна швидше досягти мети, якщо звернутися, наприклад, по ламаній АЕС.
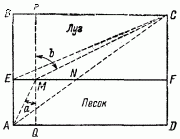
Рішення задачі про кавалеристе. Якнайшвидший шлях АМС.
На першому рисунку зазначено, що ширина піщаної смуги 2 км, луговий - 3 км, а відстань ВС - 7 км. Тоді вся довжина AC дорівнює, за теоремою Піфагора, √(52 + 72) = √74 = 8,60 км. Частина AN - шлях по піску - цього відрізка становить, як легко зміркувати, 2/5 цієї величини, тобто 3,44 км. Так як по піску рух відбувається удвічі повільніше, ніж по лузі, то 3,44 км піщаного шляху рівнозначні, в сенсі необхідного часу, 6,88 км по лузі. І, отже, весь змішаний шлях по прямій АС, рівний 8,60 км, відповідає 12,04 км шляху по лузі.
Зробимо таке ж "приведення до лугу" і для ламаного шляху АЕС. Частина АЕ = 2 км і відповідає 4 км шляху по лузі. Частина ЄС = √(32 + 72) = √(58) = 7,61 км. Разом увесь ламаний шлях AEC відповідає 4 + 7,61 = 11,61 км.
Отже, "короткий" прямий шлях відповідає 12,04 км руху по лузі, а "довгий" ламаний - всього лише 11,61 км з тієї ж ґрунті. "Довгий" шлях, як бачите, дає вигоду в 12,04 - 11,61 = 0,43, майже в півкілометра!
Але ми не вказали ще самого швидкого шляху. Найшвидший шлях, як вчить теорія, буде той, при якому (нам доведеться тут звернутися до послуг тригонометрії) синус кута b відноситься до синуса кута A, як швидкість на лузі відноситься до швидкості на піску, тобто як 2:1. Іншими словами, потрібно вибрати напрямок так, щоб sin b був вдвічі більше sin а. Для цього потрібно переступити межу між смугами в такій точці m, яка знаходиться в одному кілометрі від Е. Дійсно, тоді sin b = 6/√(32 + 62), sin a = 1/√(1 + 22 ), ставлення sin b / sin a= 6 / √45 / 1 / (3*√5) = (6/(3*√5) / (1/√5) = 2, тобто як раз відношенню швидкостей.
А яка буде в такому випадку "наведена до лугу" довжина шляху? Обчислимо: AM = √(22 + 12). що відповідає 4,47 км шляху по лузі. МС = √45 = 6,71 км. Довжина всього шляху 4,47 + 6,71 = 11,18, тобто на 860 км коротше прямолінійного шляху, який, як ми вже знаємо, відповідає 12,04 км.
Ви бачите, які вигоди приносить при даних умовах изламывание шляху. Світловий промінь якраз і обирає такий швидкий шлях, тому що закон заломлення світла суворо задовольняє вимогу математичного розв'язання задачі: синус кута заломлення відноситься до синуса кута падіння, як швидкість світла в новому середовищі до швидкості його в покидаемой середовищі; з іншого боку, це відношення дорівнює показнику заломлення світла у вказаних середовищах.
Об'єднуючи в одне правило особливості відображення і заломлення, ми можемо сказати, що світловий промінь у всіх випадках слід по якнайшвидшому шляху, тобто підкоряється правилу, яку фізики називають "принципом якнайшвидшого приходу" (принцип Ферма).
Якщо середовище неоднорідна і її заломлююча здатність змінюється поступово, як, наприклад, в нашій атмосфері, то і в такому випадку цілком здійснюється якнайшвидший прихід. Цим пояснюється те невелике викривлення променів небесних світил в атмосфері, яке на мові астрономів називається "атмосферної рефракцією". В атмосфері, поступово уплотняющейся донизу, промінь світла згинається так, що стискають його звернена до Землі. Тоді промінь довше залишається у високих шарах, які слабше уповільнюють його шлях, і проводить менше часу в "повільних" низьких шарах, у підсумку він приходить до мети швидше, ніж шляхом строго прямолінійним.
Принцип якнайшвидшого приходу (принцип Ферма) справедливий не для одних лише світлових явищ: йому повною мірою підпорядковується також поширення звуку і всіх взагалі хвилеподібних рухів, яка б не була природа цих хвиль.
Читач, без сумніву, бажав би дізнатися, чим пояснюється це властивість хвилеподібних рухів. Наведу тому відносяться сюди міркування, висловлені видатним сучасним фізиком Шредінгер (доповіді, прочитаній у Стокгольмі при отриманні Нобелівської премії 1933 р.). Він виходить з знайомого вже нам приклад марширують солдатів і має на увазі випадок руху світлового променя в середовищі поступово змінюється щільності.
“Нехай, - пише він, - для того, щоб зберегти сувору правильність фронту, солдати з'єднані довгою жердиною, який кожен з них міцно утримує в руках. Команда говорить: всім бігти якомога швидше! Якщо характер грунту повільно змінюється від точки до точки, то спочатку, скажімо, праве, а потім ліве крило фронту буде посуватися швидше - і поворот фронту здійсниться сам собою. Ми зауважимо при цьому, що пройдений шлях не прямолінійний, а викривлений. Те, що шлях цей строго співпадає з найкоротшим в сенсі часу прибуття в цей пункт при заданих властивостях ґрунту, - досить зрозуміло, так як адже кожен солдат намагався посуватися як можна швидше".