Ми знаємо, що в однорідному середовищі світло поширюється прямолінійно, тобто якнайшвидшим шляхом. Але світло обирає якнайшвидший шлях також і в тому випадку, коли не йде від однієї точки до іншої безпосередньо, а досягає її, попередньо відбившись від дзеркала.
Простежимо за його шляхом. Нехай літера A на малюнку 1обозначает джерело світла, лінія MN - дзеркало, а лінія АВС - шлях променя від свічки до ока C. Пряма KB перпендикулярна до MN.
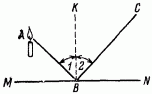
Рис. 1. Кут відбиття 2 дорівнює куту падіння 1.
За законами оптики кут відбиття 2 дорівнює куту падіння 1. Знаючи це, легко довести, що з усіх можливих шляхів від A до C, з одночасним досягненням дзеркала MN, шлях АВС - самий швидкий. Для цього порівняємо шлях променя АВС з яким-небудь іншим, наприклад з ADC (рис. 2). Опустимо перпендикуляр АЕ з точки A MN і продовжимо його далі до перетину з продовженням променя ВС в точці F. З'єднаємо точку F і D. Переконаємося, перш за все, у рівності трикутників ABE і EBF. Вони - прямокутні, і у них спільний катет ЕВ; крім того, кути EFB і ЕАР рівні між собою, так як відповідно дорівнюють кутам 2 і 1. Отже, AE = EF. Звідси випливає рівність прямокутних трикутників AED і EDF за двома катетам і, отже, рівність AD і DF.
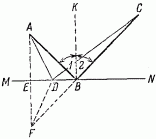
Світло, відбиваючись, обирає найкоротший шлях.
Зважаючи на це, ми можемо шлях АВС замінити рівним йому шляхом CBF (так як AB = FB), a шлях ADC - шляхом CDF. Порівнюючи між собою довжини CBF і CDF, бачимо, що пряма лінія CBF коротше ламаної CDF. Звідси шлях АВС коротший ADC, що і потрібно було довести!
Де б не знаходилася точка D, шлях АВС завжди буде коротше шляху ADC, якщо тільки кут відбиття дорівнює куту падіння. Значить, світ дійсно обирає самий короткий і найбільш швидкий шлях з усіх можливих між джерелом, дзеркалом і оком. На цю обставину вперше вказав ще Герон Олександрійський, чудовий грецький механік і математик II століття.