1865 - 1870 рр. з'явився у Франції фантастичний роман Жюля Верна "З гармати на Місяць", в якому висловлена надзвичайна думка: послати на Місяць велетенський гарматний снаряд-вагон з живими людьми! Жюль Верн представив свій проект в такій правдоподобном вигляді, що у більшості читачів, напевно, виникало питання: не можна чи справді здійснити цю думку? Про це цікаво поговорити [Тепер, після запуску штучних супутників Землі та космічних ракет, ми можемо сказати, що для космічних подорожей будуть використовуватися ракети, а не снаряди. Однак рух ракети, після того як спрацювала її остання щабель, підкоряється тим же законам, що й рух артилерійського снаряда. Тому текст автора не застарів. (Прим. ред.)].
Спочатку розглянемо, чи можна - хоча б теоретично - вистрілити з гармати так, щоб снаряд ніколи не впав назад, на Землю. Теорія допускає таку можливість. У насправді, чому снаряд, горизонтально викинутий гарматою, зрештою падає на Землю? Тому що Земля, притягаючи снаряд, викривляє його шлях: він летить не по прямій лінії, а по кривій, спрямованої до Землі, і тому рано або пізно зустрічається з грунтом. Земна поверхня, правда, теж викривлена, але шлях снаряда згинається набагато крутіше. Якщо ж кривизну шляху снаряда послабити і зробити її однаковою з викривленням поверхні земної кулі, то такий снаряд ніколи не зможе впасти на Землю! Він буде рухатися по кривій, концентричній з окружністю земної кулі; іншими словами, стане її супутником, як би другий Місяцем.
Але як домогтися, щоб снаряд, викинутий гарматою, йшов по дорозі, менш викривленого, ніж земна поверхня? Для цього необхідно лише повідомити йому достатню швидкість. Зверніть увагу на малюнок, що зображає розріз частині земної кулі.
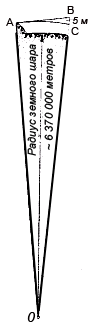
Обчислення швидкості снаряда, який повинен назавжди покинути Землю.
Залишається обчислити відрізок АВ, тобто той шлях, який проходить снаряд в секунду по горизонтальному напрямку; ми дізнаємося тоді, з якою секундної швидкістю потрібно для нашої мети викинути снаряд з жерла гармати. Обчислити це, неважко трикутника АОВ, в якому ОА - радіус земної кулі (близько 6 370 000 м); ОС = ОА, ВС = 5 м; отже, 0В = 6 370 005 м. Звідси за теоремою Піфагора маємо: (AB)2 = (6 370 005)2 - (6 370 000)2.
Зробивши обчислення, знаходимо, що шлях AB дорівнює приблизно 8 км.
Отже, якщо б не було повітря, який сильно заважає швидкому руху, снаряд, викинутий горизонтально з гармати зі швидкістю 8 км/сек, ніколи не впав би на Землю, а вічно кружляв навколо неї, подібно супутнику.
А якщо викинути снаряд з гармати з ще більшою швидкістю, - куди він полетить? В небесній механіці доводиться, що при швидкості 8, 9, 10 км/сек снаряд, вилетівши з жерла гармати, повинен описувати навколо земної кулі еліпс тим більш витягнутий, чим більше початкова швидкість. При швидкості ж снаряда 11,2 км/сек він замість еліпса опише вже незамкнену криву - параболу, назавжди віддаляючись від Землі.
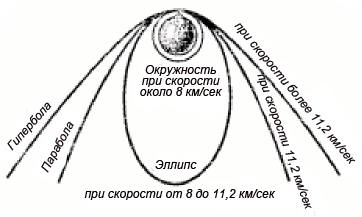
Доля гарматного снаряда, випущеного з початковою швидкістю 8 км/с і більше.
Ми бачимо, отже, що теоретично мислимо полетіти на Місяць всередині снаряда, викинутого з досить великою швидкістю.
(Попереднє міркування мало на увазі атмосферу, не перешкоджає руху снарядів. В реальних умовах наявність чинить опір атмосфери надзвичайно ускладнило б отримання таких високих швидкостей, а бути може, зробила б їх абсолютно недосяжними.)